Cách tìm cực trị của hàm số qua 2 quy tắc
Hướng dẫn học sinh lớp 12 cách tìm cực trị (cực đại, cực tiểu) của hàm số qua 2 quy tắc mà Gia sư Tiến Bộ chia sẻ dưới đây.
Trước tiên chúng ta cần ôn lại lý thuyết thế nào là giá trị cực đại, cực tiểu của hàm số.
Khái niệm cực trị
Cho hàm số ![]()
a) Hàm số ![]() đạt cực đại tại
đạt cực đại tại ![]()
![]()
Khi đó ![]() là giá trị cực đại của hàm số.
là giá trị cực đại của hàm số.
b) Hàm số ![]() đạt cực tiểu tại
đạt cực tiểu tại ![]()
![]()
Khi đó ![]() là giá trị cực tiểu của hàm số.
là giá trị cực tiểu của hàm số.
* Chú ý:
a) Cần phân biệt các các khái niệm:
– Giá trị cực trị của hàm số.
Các định lý về cực trị:
Định lý 1:
Giả sử hàm số ![]() liên tục trên khoảng
liên tục trên khoảng ![]() và có đạo hàm trên
và có đạo hàm trên ![]() hoặc
hoặc ![]() .
.
a) Nếu![]() thì
thì ![]() là một điểm cực đại của hàm số.
là một điểm cực đại của hàm số.
b) Nếu ![]() thì
thì ![]() là một điểm cực tiểu của hàm số.
là một điểm cực tiểu của hàm số.
* Chú ý: Hàm số có thể đạt cực trị tại những điểm mà tại đó đạo hàm không xác định.
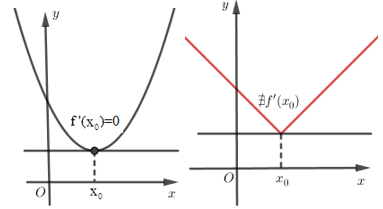
Định lý 2:
Giả sử hàm số ![]() liên tục trên khoảng
liên tục trên khoảng ![]() và có đạo hàm trên
và có đạo hàm trên ![]() hoặc
hoặc ![]() .
.
a) Nếu![]() thì
thì ![]() là một điểm cực đại của hàm số.
là một điểm cực đại của hàm số.
b) Nếu ![]() thì
thì ![]() là một điểm cực tiểu của hàm số.
là một điểm cực tiểu của hàm số.
* Chú ý: Hàm số có thể đạt cực trị tại những điểm mà tại đó đạo hàm không xác định.

Định lý 2:
Giả sử ![]() có đạo hàm cấp 2 trong
có đạo hàm cấp 2 trong ![]() .
.
a) Nếu![]() thì
thì ![]() là một điểm cực tiểu của hàm số.
là một điểm cực tiểu của hàm số.
b) Nếu![]() thì
thì ![]() là một điểm cực đại của hàm số.
là một điểm cực đại của hàm số.
Cách tìm cực trị của hàm số
Phương pháp:
Quy tắc tìm cực trị số 1:
– Bước 1: Tìm tập xác định của hàm số.
– Bước 2: Tính ![]() , tìm các điểm tại đó
, tìm các điểm tại đó ![]() hoặc không xác định.
hoặc không xác định.
– Bước 3: Lập bảng biến thiên và kết luận.
+ Tại các điểm mà đạo hàm đổi dấu từ âm sang dương thì đó là điểm cực tiểu của hàm số.
+ Tại các điểm mà đạo hàm đổi dấu từ dương sang âm thì đó là điểm cực đại của hàm số.
Quy tắc tìm cực trị số 2:
– Bước 1: Tìm tập xác định của hàm số.
– Bước 2: Tính ![]() , giải phương trình
, giải phương trình ![]() và kí hiệu
và kí hiệu ![]() là các nghiệm của nó.
là các nghiệm của nó.
– Bước 3: Tính ![]() và
và ![]() .
.
– Bước 4: Dựa và dấu của ![]() suy ra điểm cực đại, cực tiểu:
suy ra điểm cực đại, cực tiểu:
+ Tại các điểm ![]() mà
mà ![]() thì đó là điểm cực tiểu của hàm số.
thì đó là điểm cực tiểu của hàm số.
+ Tại các điểm ![]() mà
mà ![]() thì đó là điểm cực đại của hàm số.
thì đó là điểm cực đại của hàm số.
* Chú ý: Đối với các bài toán tìm cực trị của hàm số lượng giác thì dùng quy tắc 2 sẽ thuận tiện hơn, tránh được việc xét dấu đạo hàm.
Bài tập tìm cực trị của hàm số
Bài 1. Tìm cực trị của hàm số ![]() .
.
Giải
Tập xác định ![]() .
.
Ta có: ![]() . Cho
. Cho ![]() .
.
Bảng biến thiên:
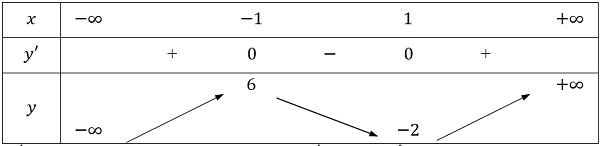
Vậy hàm số đạt cực đại tại ![]() và hàm số đạt cực tiểu tại
và hàm số đạt cực tiểu tại ![]() .
.
Bài 2. Tìm cực trị của hàm số ![]() .
.
Giải
Tập xác định ![]() .
.
Ta có: ![]() . Cho
. Cho ![]()
Bảng biến thiên:
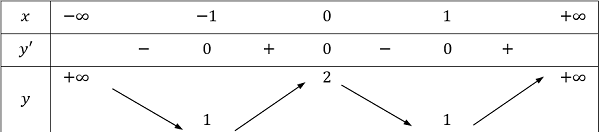
Vậy hàm số đạt cực tiểu tại ![]() và hàm số đạt cực đại tại
và hàm số đạt cực đại tại ![]() .
.
Bài 3. Tìm cực trị của hàm số ![]()
Giải
Tập xác định ![]() .
.
Ta có: ![]()
Bảng biến thiên:
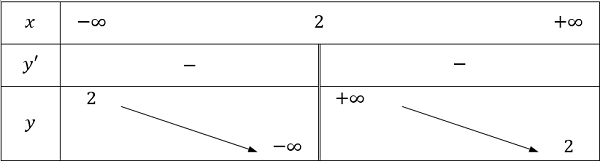
Vậy hàm số đã cho không có cực trị.
Giải tích 12 - Tags: cực đại, cực tiểu, cực trị, toán 12