Giải bài toán cực trị bằng tích vô hướng của 2 vectơ
Phương pháp giải bài toán cực trị bằng tích vô hướng
Sử dụng tích vô hướng biến đổi biểu thức cần tìm cực trị về biểu thức độ dài, ví dụ: ![]()
Khi đó ![]()
MI=0 ⇔ M≡I.
Ứng dụng tích vô hướng giải các bài toán cực trị
Bài toán 1: Cho ![]()
a. CMR: ![]() .
.
b. CMR: ![]() , từ đó suy ra vị trí của M để
, từ đó suy ra vị trí của M để ![]() đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất.
Giải
a. Ta có:
![]()
![]()
b. Ta có:
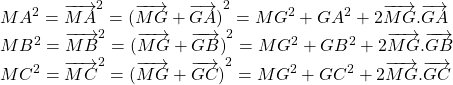
Cộng vế theo vế ta được:
![]()
![]() (vì
(vì ![]() )
)
Từ đó suy ra ![]() đạt giá trị nhỏ nhất khi
đạt giá trị nhỏ nhất khi ![]()
Bài toán 2: Cho hình bình hành ABCD, tâm O, M là điểm tùy ý.
a. CMR: ![]()
b. Giả sử M di động trên đường tròn (d), xác định vị trí của M để ![]() đạt giá trị nhỏ nhất.
đạt giá trị nhỏ nhất.
Giải
a. Ta có:
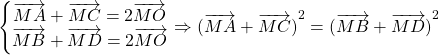
![]() (1)
(1)
Ta xét:
![]()
![]()
![]() (2)
(2)
Thay (2) vào (1), ta được:
![]()
![]() ⇒ đpcm.
⇒ đpcm.
b. Từ kết quả câu a) suy ra ![]() đạt giá trị nhỏ nhất khi và chỉ khi
đạt giá trị nhỏ nhất khi và chỉ khi ![]() nhỏ nhất
nhỏ nhất
⇔ M là hình chiếu vuông góc của D lên (d).
Bài tập tự giải
Bài 1: Cho ![]()
a. Tìm giá trị nhỏ nhất của S.
b. Tìm giá trị lớn nhất của S.
Bài 2: Cho ![]()
a. CMR vectơ ![]() , không phụ thuộc vào vị trí của M.
, không phụ thuộc vào vị trí của M.
b. Gọi O là tâm đường tròn ngoại tiếp ![]()
![]()
c. Tìm tập hợp những điểm M thỏa mãn ![]() =0.
=0.
Giả sử M di động trên đường tròn ngoại tiếp ![]()