Góc nội tiếp đường tròn, tính chất và áp dụng vào giải toán
Góc nội tiếp là gì? Áp dụng tính chất góc nội tiếp để chứng minh tứ giác nội tiếp đường tròn qua một số bài tập có lời giải.
Trong chương trình toán lớp 9 có rất nhiều bài toán liên quan tới góc nội tiếp trong đường tròn.
Khái niệm góc nội tiếp
Góc nội tiếp là góc có đỉnh nằm trên đường tròn và có hai cạnh là hai dây cung của đường tròn đó.
Tính chất góc nội tiếp đường tròn
Trong một đường tròn:
– Các góc nội tiếp cùng chắn một cung thì bằng nhau.
– Các góc nội tiếp chắn các cung bằng nhau thì bằng nhau.
– Góc nội tiếp chắn nửa đường tròn bằng 90 độ (1 góc vuông).
Bài tập áp dụng
Để làm được những bài tập dưới đây chúng ta cần sử dụng các tính chất của góc nội tiếp. Các em tự làm bài sau đó đối chiếu với cách giải.
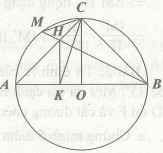
Bài 1. Cho đường tròn (O, R) có đường kính AB. Bán kính CO vuông góc với AB, M là một điểm bất kì trên cung nhỏ AC (M khác A, C); BM cắt AC tại H. Gọi K là hình chiếu của H trên AB.
a. Chứng minh CBKH là tứ giác nội tiếp.
b. Chứng minh CA là tia phân giác của góc MCK.
Giải
a. Ta có: góc HCB bằng 90º (do chắn nửa đường tròn đường kính AB)
góc HKB bằng 90º (do K là hình chiếu của H trên AB)
Nên tứ giác CBKH nội tiếp trong đường tròn đường kính HB.
b. Ta có:
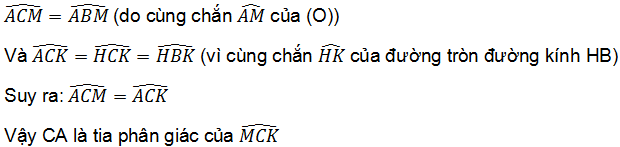
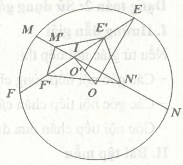
Bài 2. Cho đường tròn (O) và điểm I ở trong đường tròn. Dựng qua I hai dây cung bất kì MIN và EIF. Gọi M’, N’, E’, F’ lần lượt là trung điểm của IM, IN, IE, IF.
a. Chứng minh tứ giác M’E’N’F’ là tứ giác nội tiếp.
b. Chứng minh IM’.IN’ = IE’.IF’.
Giải
a. Gọi trung điểm của OI là O’
⇒ O’E’ là đường trung bình của tam giác IOE.
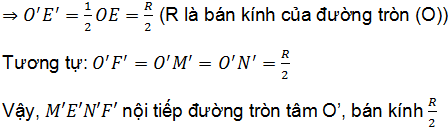
b. Tứ giác M’E’N’F’ nội tiếp suy ra:
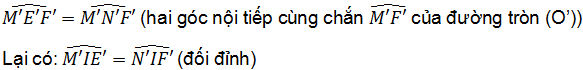
⇒ △M’IE’ đồng dạng △F’IN’ (g.g)
Bài 3. Từ đỉnh A của hình vuông ABCD kẻ hai tia tạo với nhau một góc 45º. Một tia cắt cạnh BC tại E cắt đường chéo BD tại P. Tia kia cắt cạnh CD tại F và cắt đường chéo BD tại Q.
a. Chứng minh 5 điểm E, P, Q, F và C cùng nằm trên một đường tròn.
b. Chứng minh:
Giải
a. Ta có:
Suy ra tứ giác ADFP nội tiếp được trong đường tròn.
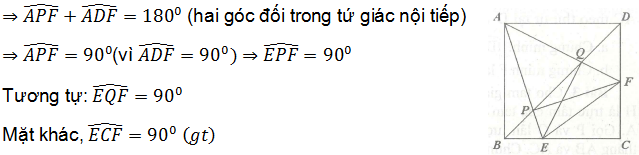
Vậy, năm điểm P, Q, F, C, E cùng thuộc đường tròn đường kính EF.
b. Theo câu a, góc AQE bằng 90º
Tương tự: △APF cũng vuông cân:
Từ (1) và (2) suy ra:
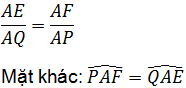
⇒ △AQP đồng dạng △AEF (c.g.c)
Bài 4. Cho hình thang ABCD (AB//CD, AB>CD) nội tiếp trong một đường tròn có số đo cung AD bằng 120º. Hai đường chéo AC và BD cắt nhau tại I. Gọi E, F, M lần lượt là trung điểm của các đoạn thẳng IA, ID, BC.
a. Chứng minh tứ giác BEFC nội tiếp được trong một đường tròn.
b. Chứng minh tam giác MEF là tam giác đều.
Giải:
a) Ta có: góc ACD là góc nội tiếp chắn cung AD của đường tròn ngoại tiếp hình thang ABCD nên:
⇒ góc BDC bằng 60º (ABCD là hình thang cân)
⇒ CF là đường cao của △ICD ⇒ CF ⊥ ID
⇒ góc CFB bằng 90º
Vậy, tứ giác BEFC nội tiếp được trong đường tròn tâm M đường kính BC.
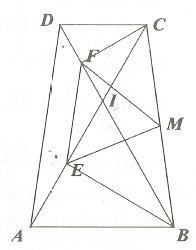
b. Ta có: tứ giác BEFC nội tiếp trong đường tròn tâm M (chứng minh trên)
Lại có: EF là đường trung bình của △IAD
Mà: AD = BC suy ra ME = MF = EF ⇒ △MEF là tam giác đều.
Bài 5. Cho đường tròn tâm O bán kính R tiếp xúc với đường thẳng d tại A. Trên d lấy điểm H không trùng với A, AH < R. Qua H kẻ đường thẳng vuông góc với d, đường thẳng này cắt đường tròn tại E và B (E nằm giữa B và H)
a. Lấy điểm C trên d sao cho H là trung điểm của AC, CE cắt AB tại K.
Chứng minh AHEK là tứ giác nội tiếp.
b. Xác định vị trí điểm H để AB = R
.
Giải:
a. Ta có: EH ⊥ AC tại trung điểm H của AC nên △AEC cân tại E.
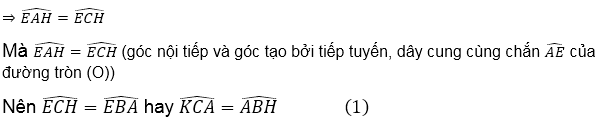
Hai tam giác AKC và AHB có:
Nên △AKC đồng dạng với △AHB
Suy ra tứ giác AHEK nội tiếp trong đường tròn đường kính AE.
b. Ta có:
Bài 6. Cho đường tròn (O) có đường kính AB = 2R và điểm C thuộc đường tròn đó (C khác A, B). Lấy điểm D thuộc dây BC (D khác B, C). Tia AD cắt cung nhỏ BC tại điểm E, tia AC cắt tia BE tại điểm F. Gọi I là tâm đường tròn ngoại tiếp tứ giác FCDE.
a. Chứng minh IC là tiếp tuyến của đường tròn (O).
b. Biết DF = R.
Giải:
a. Ta có: góc DCF bằng 90º; góc DEF bằng 90º
Suy ra, tâm I của đường tròn ngoại tiếp tứ giác CDEF là trung điểm của DF.
⇒ IC = IF (bán kính)
Tứ giác CDEF nội tiếp nên:
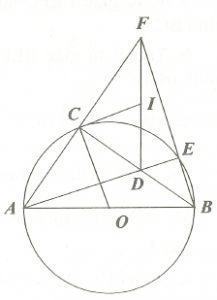
Vậy, IC là tiếp tuyến của đường tròn (O).
b. Chứng minh tương tự câu a, ta được: IE là tiếp tuyến của đường tròn (O)
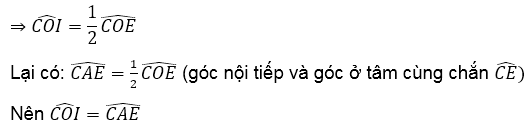
Suy ra hai tam giác vuông ICO và FEA đồng dạng với nhau.
Bài 7. Cho đường tròn tâm O đường kính AB = 2R. Gọi d1 và d2 lần lượt là hai tiếp tuyến của đường tròn (O) tại A và B. Gọi I là trung điểm của OA và E là điểm thuộc đường tròn (O) (E khác A, B). Đường thẳng d đi qua E và vuông góc với EI cắt hai đường thẳng d1 và d2 lần lượt tại M và N.
a. Chứng minh MI là tiếp tuyến của đường tròn ngoại tiếp tứ giác BHEI.
b. Chứng minh AM.BN = AI.BI
Giải:
a. Góc NBI và góc NEI đều bằng 90º nên đường tròn ngoại tiếp tứ giác BNEI có đường kính là NI
Tứ giác AMEI nội tiếp
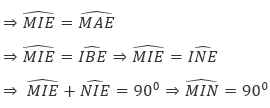
Vậy, MI là tiếp tuyến của đường tròn ngoại tiếp tứ giác BNEI.
b. △MAI đồng dạng với △IBN
Bài 8. Cho đường tròn (O) và dây cung AB. M là điểm chính giữa của cung AB. Hai cát tuyến vẽ từ M cắt đường tròn (O) tại C và E, cắt đường thẳng AB tại D và F.
a. Chứng minh tứ giác CDFE nội tiếp được đường tròn.
b. Chứng minh đường tròn ngoại tiếp tam giác ACD tiếp xúc với AM.
c. Tìm tập hợp tâm của đường tròn ngoại tiếp tam giác ACD.
Giải:
a. góc DCE là góc nội tiếp chắn cung MBE của đường tròn (O) nên:
Góc BFE là góc có đỉnh ở bên trong đường tròn (O) nên:
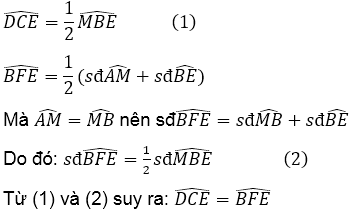
Vậy, tứ giác CDFE nội tiếp được đường tròn.
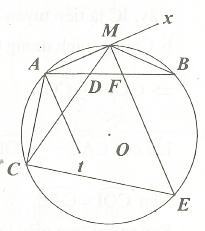
b. Ta có:
Qua A vẽ tiếp tuyến Ax của đường tròn ngoại tiếp △ACD, ta có:
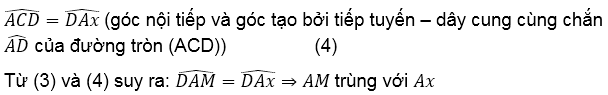
⇒ AM là tiếp tuyến của đường tròn ngoại tiếp △ACD.
c. Theo chứng minh trên AM là tiếp tuyến tại A của đường tròn ngoại tiếp △ACD nên tâm I thuộc đường thẳng vuông góc với AM tại A.
Vậy, tập hợp điểm tâm của đường tròn ngoại tiếp tam giác ACD là tia At vuông góc với AM tại A.
Bài 9. Cho tam giác ABC vuông tại A, trên cạnh AC lấy điểm D (D khác A, D khác C). Đường tròn (O) đường kính DC cắt BC tại E (E khác C).
a. Chứng minh tứ giác ABED nội tiếp đường tròn.
b. Đường thẳng BD cắt đường tròn (O) tại điểm thứ hai I. Chứng minh ED là tia phân giác của góc AEI.
c. Giả sử tan góc ABC = 
K A^{2}=K N . F P
O Q^{2}=O I . O A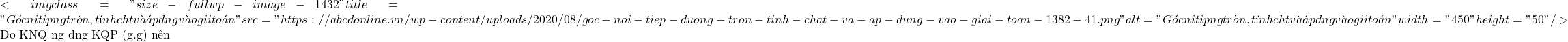
K Q^{2}=K N . K P
A K^{2}=N K . K P
A C^{2}=A B^{2}-B C^{2}=4 R^{2}-R^{2}=3 R^{2}
A C=R \sqrt{3}
\displaystyle \sqrt{3}$
Dễ thấy:
Trong tam giác vuông IBM: góc I bằng 90º ta có:
Tứ giác QAIM là hình tháng vuông vì AQ // IM, góc I bằng 90º
Do đó, diện tích hình thang vuông QAIM bằng:
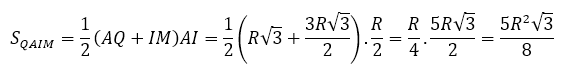
Bài 13. Cho đường tròn tâm O đường kính AB và điểm C trên đường tròn sao cho CA = CB. Gọi M là trung điểm của AC, nối BM cắt cung AC tại E, AE và BC kéo dài cắt nhau tại D.
a. Chứng minh: DE.DA = DC.DB.
b. Chứng minh: MOCD là hình bình hành.
c. Kẻ EF vuông góc với AC. Tính tỷ số ME/EF ?
d. Vẽ đường tròn tâm E bán kính EA cắt đường tròn (O) tại điểm thứ hai là N; EF cắt AN tại I, cắt đường tròn (O) tại điểm thứ hai là K; EB cắt AN tại H. Chứng minh tứ giác BHIK nội tiếp được đường tròn.
Giải:
a. Chứng minh DE.DA = DC.DB
Ta có: góc ACB bằng 90º (góc nội tiếp chắn nửa đường tròn (O))
⇒ góc ACD bằng 90º (vì kề bù với góc ACB)
Ta lại có: góc AEB bằng 90º (góc nội tiếp nửa đường tròn (O))
⇒ góc DEB bằng 90º (vì kề bù với góc AEB)
Xét △ADC và △BDE có:
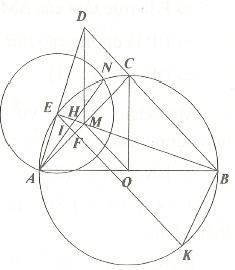
b. Chứng minh MOCD là hình bình hành
Ta có: MC = MA (gt)
⇒ OM ⊥ AC (liên hệ giữa đường kính và dây cung)
CD ⊥ AC (vì góc ACD bằng 90º)
⇒ OM // CD (cùng vuông góc với AC) (1)
Mặt khác: △DAB có BE và AC là hai đường cao cắt nhau tại M
⇒ M là trực tâm △DAB
⇒ DM là đường cao thứ ba ⇒ DM ⊥ AB
Mà: cung CA = cung CB (vì CA = CB) ⇒ CO ⊥ AB
Suy ra: DM // CO (2)
Từ (1) và (2) suy ra: tứ giác MOCD là hình bình hành.
c. Kẻ EF ⊥ AC. Tính tỉ số MF/EF.
Xét △MFE và △MCB có:
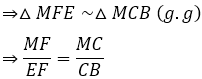
Ta lại có: AC = 2MC (gt)
Mà: CB = CA ⇒ CB = 2MC
Suy ra:
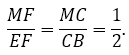
d. Chứng minh tứ giác BHIK nội tiếp được đường tròn
Ta có:
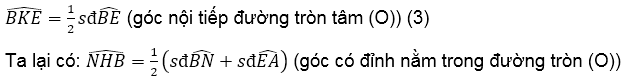
Mà: EA = EN (bán kính đường tròn (E))
⇒ cung EA bằng cung EN
Suy ra:
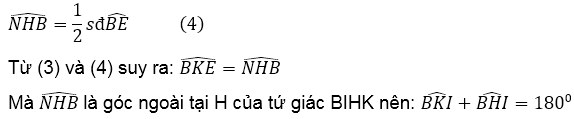
Vậy, tứ giác BIHK nội tiếp được đường tròn.
Hình học 9 - Tags: góc, góc nội tiếp, nội tiếp, nội tiếp đường tròn, toán 9, tứ giác, tứ giác nội tiếp