Sự đồng biến, nghịch biến của hàm số

Hàm số đơn điệu (đồng biến, nghịch biến) khi nào? Đồ thị hàm số đi lên, đi xuống. Các dạng toán liên quan thường gặp.

Trong bài viết này có lý thuyết sự đồng biến, nghịch biến của hàm số và các dạng bài tập có liên quan.

1. Định nghĩa

Cho hàm số y=f(x)

 xác định trên K (K có thể là một khoảng, đoạn hoặc nửa khoảng)

– Hàm số y=f(x)

được gọi là đồng biến trên K nếu:

\forall x_{1}, x_{2} \in K: x_{1}<x_{2} \Rightarrow f\left(x_{1}\right)<f\left(x_{2}\right)

. Đồ thị đi lên từ trái sang phải.

– Hàm số y=f(x)

được gọi là nghịch biến trên K nếu:

\displaystyle \forall x_{1}, x_{2} \in K: x_{1}<x_{2} \Rightarrow f\left(x_{1}\right)>f\left(x_{2}\right). Đồ thị đi xuống từ trái sang phải.

2. Định lí

Cho hàm số y=f(x)

xác định và có đạo hàm trên K

a) Nếu f^{\prime}(x)>0, \forall x \in K thì hàm số y=f(x)

đồng biến trên K

b) Nếu f^{\prime}(x)<0, \forall x \in K thì hàm số y=f(x)

nghịch biến trên K

Định lý mở rộng: Giả sử hàm số y=f(x)

có đạo hàm trên K

a) Nếu f^{\prime}(x) \geq 0, \forall x \in K và f^{\prime}(x)=0 chỉ tại một số hữu hạn điểm thì hàm số đồng biến trên K

b) Nếu f^{\prime}(x) \leq 0, \forall x \in K và f^{\prime}(x)=0 chỉ tại một số hữu hạn điểm thì hàm số nghịch biến trên K

3. Một số chú ý

Dưới đây là những chú ý về tính đồng biến, nghịch biến mà các em cần biết.

– Nếu hàm số f(x) và g(x) cùng đồng biến (nghịch biến) trên K thì hàm số f(x)+g(x) cũng đồng biến (nghịch biến) trên K. Tính chất này có thể không đúng đối với hiệu f(x)-g(x).

– Nếu hàm số f(x) và g(x) là các hàm số dương và cùng đồng biến (nghịch biến) trên K thì hàm số f(x) \cdot g(x) cũng đồng biến (nghịch biến) trên K. Tính chất này có thể không đúng khi f(x), g(x) không là các hàm số dương trên K.

– Cho hàm số u=u(x), xác định với x \in(a ; b) và u(x) \in(c ; d) . Hàm số f[u(x)] cũng xác định với x \in(a ; b).

4. Các dạng toán thường gặp

Dạng 1: Tìm các khoảng đơn điệu của hàm số

Phương pháp:

– Bước 1: Tìm TXĐ của hàm số.

– Bước 2: Tính đạo hàm f^{\prime}(x), tìm các điểm x_{1}, x_{2}, \ldots, x_{n} mà tại đó đạo hàm bằng Rendered by QuickLaTeX.com hoặc không xác định.

– Bước 3: Xét dấu đạo hàm và nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.

+ Các khoảng mà f^{\prime}(x)>0 là các khoảng đồng biến của hàm số.

+ Các khoảng mà f^{\prime}(x)<0 là các khoảng nghịch biến của hàm số.

Ví dụ 1: Tìm khoảng đồng biến, nghịch biến của hàm số y = 2{x^4} + 1.

Ta có y^{\prime}=8 x^{3}, y^{\prime}>0 \Leftrightarrow x>0 nên hàm số đã cho đồng biến trên (0 ;+\infty)

y^{\prime}<0 \Leftrightarrow x<0 nên hàm số đã cho nghịch biến trên (-\infty ; 0)
Một số trường hợp đặc biệt:

Sự đồng biến, nghịch biến của hàm số

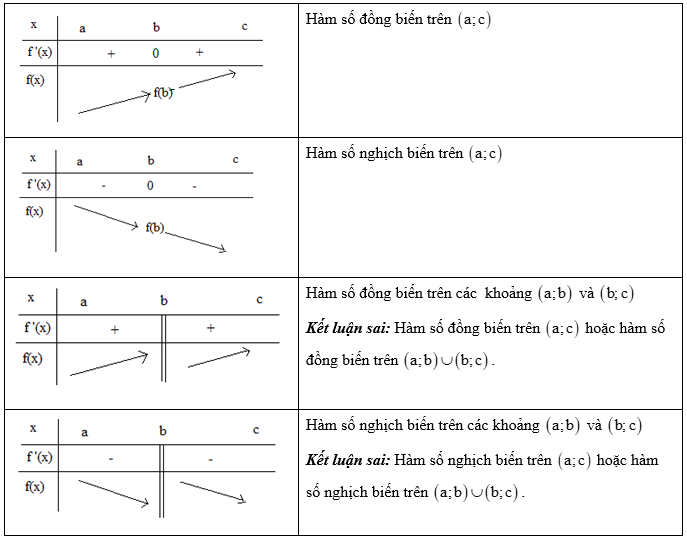
Dạng 2: Tìm giá trị của m để hàm số đơn điệu trên R

Phương pháp:

– Bước 1: Tính f'\left( x \right).

– Bước 2: Nêu điều kiện của bài toán:

+ Hàm số y = f\left( x \right) đồng biến trên R \Leftrightarrow y' = f'\left( x \right) \geqslant 0,\forall x \in R và y' = 0 tại hữu hạn điểm.

+ Hàm số y = f\left( x \right) nghịch biến trên R \Leftrightarrow y' = f'\left( x \right) \leqslant 0,\forall x \in R và y' = 0 tại hữu hạn điểm.

– Bước 3: Từ điều kiện trên sử dụng các kiến thức về dấu của nhị thức bậc nhất, tam thức bậc hai để tìm m.

Cho hàm số f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right). Khi đó:

f(x) \geqslant 0, \forall x \in R \Leftrightarrow\left\{\begin{array}{l}a>0 \\ \Delta \leqslant 0\end{array}\right.

f(x) \leqslant 0, \forall x \in R \Leftrightarrow\left\{\begin{array}{l}a<0 \\ \Delta \leqslant 0\end{array}\right.

Dạng 3: Tìm m để hàm số đơn điệu trên miền D cho trước

Phương pháp:

– Bước 1: Nêu điều kiện để hàm số đơn điệu trên D:

+ Hàm số y = f\left( x \right) đồng biến trên D \Leftrightarrow y' = f'\left( x \right) \geqslant 0, \forall x \in D.

+ Hàm số y = f\left( x \right) nghịch biến trên D \Leftrightarrow y' = f'\left( x \right) \leqslant 0, \forall x \in D.

– Bước 2: Từ điều kiện trên sử dụng các cách suy luận khác nhau cho từng bài toán để tìm m.

– Bước 3: Kết luận.

Dạng 4: Tìm m để hàm số 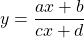\displaystyle y=\frac{a x+b}{c x+d} đồng biến, nghịch biến trên khoảng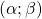 (\alpha ; \beta)

– Bước 1: Tính y^{\prime}.

– Bước 2: Nêu điều kiện để hàm số đồng biến, nghịch biến:

+ Hàm số đồng biến trên \displaystyle (\alpha ; \beta) \Leftrightarrow\left\{\begin{array}{l}y^{\prime}=f^{\prime}(x)>0, \forall x \in(\alpha ; \beta) \\ -\frac{d}{c} \notin(\alpha ; \beta)\end{array}\right.

+ Hàm số nghịch biến trên \displaystyle (\alpha ; \beta) \Leftrightarrow\left\{\begin{array}{l}y^{\prime}=f^{\prime}(x)<0, \forall x \in(\alpha ; \beta) \\ -\frac{d}{c} \notin(\alpha ; \beta)\end{array}\right.

– Bước 3: Kết luận.

Giải tích 12 - Tags: , , , ,